
Mouvement sinusoidal
Calcul du cylindre hydraulique, du cylindre oscillant
L'oscillation sinusoïdale harmonique d'un axe de vérin régulé la plus simple est une course cyclique de tige de piston. Mais même des profils de conduite totalement irréguliers peuvent être décrits mathématiquement en appliquant un mouvement sinusoïdal à chaque point.
Le calcul simplifié intégré dans le configurateur de produits HäKo (Vérin d'essais >> Calculation hydraulique) est utilisé pour concevoir le mouvement dynamique en opération sinusoïdale. Les données relatives aux vérins sont avant tout prises en compte. Les autres composants du système, tels que les tuyaux ou les vannes et leurs fuites, ne sont pas couverts.
Le mouvement sinusoïdal est défini en entrant l'amplitude et la fréquence. Ainsi, le calcul détermine les valeurs maximales correspondantes du mouvement, qui, dans le cas d'une oscillation sinusoïdale ne se présentent pas en même temps. Par exemple, la vitesse a sa valeur maximale au moment où la valeur de l'accélération est zéro.
Ceci est suffisant pour déterminer la dimension du vérin pour une conception typique.
Ce calcul ne remplace pas la simulation du système hydraulique complet, qui est nécessaire dans des cas spéciaux, par exemple lorsque le système atteint ses limites de conception.
Le calcul est utilisé pour dimensionner un mouvement en opération sinusoïdale. Il ne prend pas en compte le cas où le système hydraulique est mis en marche ou arrêté.
Calcul des forces
La force de vérin Fb avec une pression de service est la force atteinte en fonctionnement dynamique. La pression de service désigne la pression réelle pb présente dans la chambre du vérin réglable derrière la valve de contrôle.
Fb = pb • A
avec la surface de piston efficace de l’alésage D2K et du diamètre de tige de piston d2s
A = π / 4 • (D2K - d2s)
La force de vérin Fs avec une pression système est la force atteinte en fonctionnement statique. La pression système désigne la pression ps présente avant la valve de contrôle mise à disposition par l'unité.
Fs = ps • A
Mouvement sinusoïdal dynamique
En fonctionnement dynamique, un mouvement sinusoïdal créé des rapports physiques entre
- l'amplitude +/- x - le mouvement de course réel pendant l'oscillation
- la vitesse v - la vitesse momentanée (et en constante évolution pendant l'oscillation) du piston
- l'accélération a - l'accélération momentanée (et en constante évolution pendant l'oscillation) du piston
- la fréquence f - la conséquence temporelle du mouvement de course, indiqué comme nombre d'oscillations par unité de temps
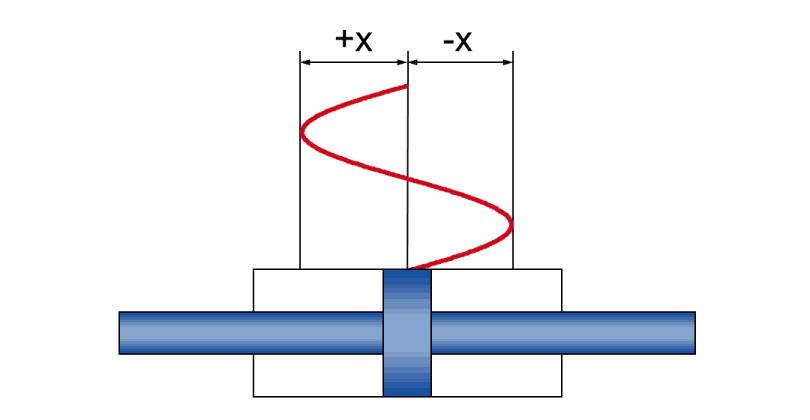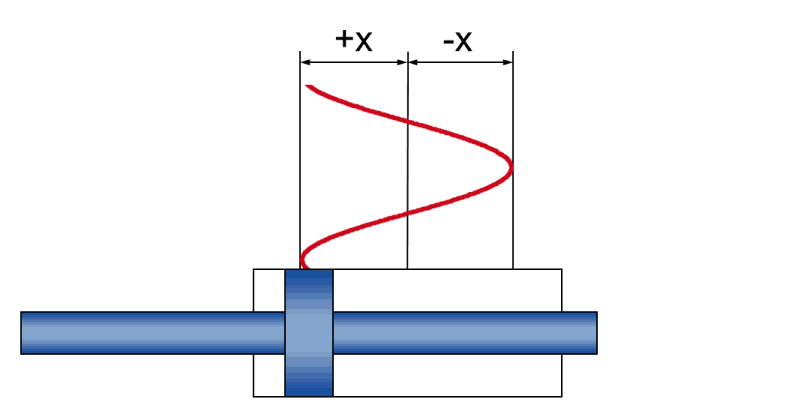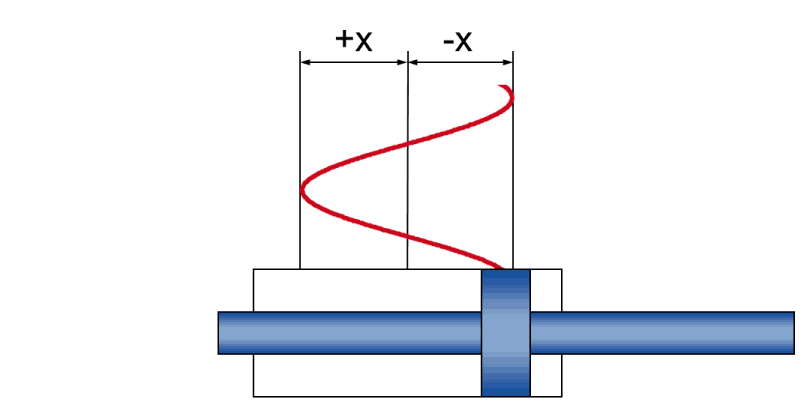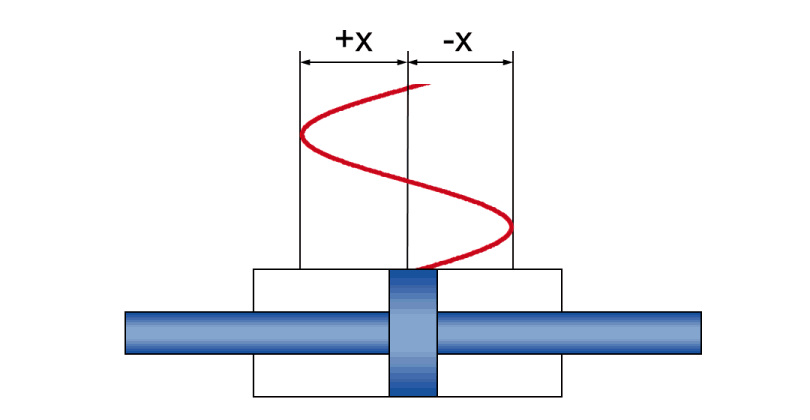
| Maximum |
| v = 2 π f x |
| a = 4 π2 f2 x |
Cela donne le débit volumétrique Q nécessaire au mouvement max.
Q = v • A
avec la surface de piston efficace A
A = π / 4 • (D2Kolben - d2Stange)
et la force d'accélération Fa que doit fournir le vérin
Fa = m • a
L'accélération maximale et la masse en mouvement calculées ici donnent la force d'accélération que doit fournir le vérin. La masse propre de la tige de piston est respectée dans le programme de calcul, les masses supplémentaires mises en mouvement doivent être indiquées dans le champ correspondant.
Recommandation pour servo valve
La pression système ps se calcule en prenant en compte la baisse de pression Δp dans la valve de contrôle :
pb = ps - Δp
La baisse de pression de la valve de contrôle est généralement de 70 bar ou de 10 bar en débit nominal avec des valves de contrôle. En fonctionnement celle-ci dépend toutefois du débit réel.
Le programme fait une proposition au débit volumétrique nécessaire concernant le débit nominal pour une éventuelle valve de contrôle. La baisse de pression est alors également calculée pour cela. Cela doit permettre d'obtenir rapidement un aperçu global de la classe de taille de valve qui serait nécessaire.
Il faut ajouter le courant d'huile de fuite du système de joints et de la valve d'assistance à la valeur calculée du débit volumétrique.
Une détermination et un réglage précis de la valve restent indépendants de ce réglage.